1. 확률분포
1. 밀도추정(Density Estimation)
밀도추정 : N개의 관찰데이터(observations) $ x_1, ... ,x_N $가 주어졌을 때 분포함수 p(X) 를 찾는 것
1.p(x)를 파라미터화된 분포로 가정한다. 회귀, 분류문제에서의 주로(p(t|x),p(C|x)를 추정한다.
2. 그 다음 분포의 파라미터를 찾는다.
빈도주의 방법(Frequentist'way) : 어떤 기준 (예를 들어 likelihood)을 최적화시키는 과정을 통해 파라미터 값을 정한다. 파라미터의 하나의 값을 구하게 된다.
베이지언 방법(Bayesian way): 먼저 파라미터의 사전확률(prior distribution)을 가정하고 Bayes'rule을 통해 파라미터의 사후확률을 구한다
3. 파라미터를 찾았다면(한 개의 값이든 분포든) 그것을 사용해 "예측"할 수 있다(t나 C).
켤레사전분포(Conjugate Prior): 사후확률이 사전확률과 동일한 함수형태를 가지도록 해준다.
2.이항 변수 :빈도주의 방법 (이산적인방법 그니깐 몇개정해져있음 동전이나 주사위)
이항 확률변수 $ x \in [0,1] $ 가 다음을 만족한다고 하자.
$ p(x = 1|\mu) = \mu,p(x = - |\mu) = 2 - \mu $
p(x)는 베르누이 분포로 표현될 수 있다.
$ Bern(x|\mu ) = \mu ^x (1- \mu ) ^{1-x} $
기댓값, 분산
$ mathbb{E} [x] = \mu $
$var[x] = \mu (1- \mu ) $
우도함수(likelihood Function) ()
x값을 N번 관찰한 결과를$ D=[ x_1, ..., x_n]$ 라고 하자. 각 x각 독립적으로$ p(x| \mu )$ 에서 뽑혀진다고 가정하면 다음과 같이 우도함수( \mu의 함수인)를 만들 수 있다.
$ p(\mathcal{D} | \mu ) = \prod^{N}_{n=1} p(x_n| \mu) = \prod ^{N} _{n=1} \mu ^{x_n}(1 - \mu)^{1-x_n} $
빈도주의 방법에서는 \mu 값을 이 우도함수를 최대화시키는 값으로 구할 수 있다
$ lnp(\mathcal{D}|\mu ) = \sum ^{N}_{n=1} p(x_n| \mu) = \sum^{N}_{n=1}\{x_n ln\mu +(1-x_n)ln(1-\mu)\} $

이런식 https://angeloyeo.github.io/2020/07/17/MLE.html
최대우도법(MLE) - 공돌이의 수학정리노트
angeloyeo.github.io
$ \mu $ 의 최대우도 추정치 는
$ \mu ^{ML} = \frac{m}{M} with m = $(#observations of x = 1 )
$ N = m = 3 \rightarrow \mu ^{ML} = 1! $
이항분포 (Binormial Distribution)
$ \mathcal{D} = \{x_1, ..., x_N \} $일 때 , 이항변수 x가 1 인경우를 m 번 관찰할 확률
$ Bin (m | N , \mu ) = \binom{N}{m} \mu ^m (1- \mu)^{N-m} $
$ \binom{N}{M} = \frac{N!}{(N-m)!m!} $
$ \mathbb{E}[m] = \sum ^{N}_{m=0} mBin(m|N, \mu ) = N \mu $
$ var[m] = \sum ^{N}_{m=0} (m - \mathbb{E} [m])^2 Bin(m|N, \mu) = N \mu ( 1- \mu ) $
이항변수 : 베이지언 방법
베타분포 ( Beta Distribution)
베이지언 방법으로 문제를 해결하기 위해 베타분포를 컬레사전분포(conjugate prior) 로 사용한다.
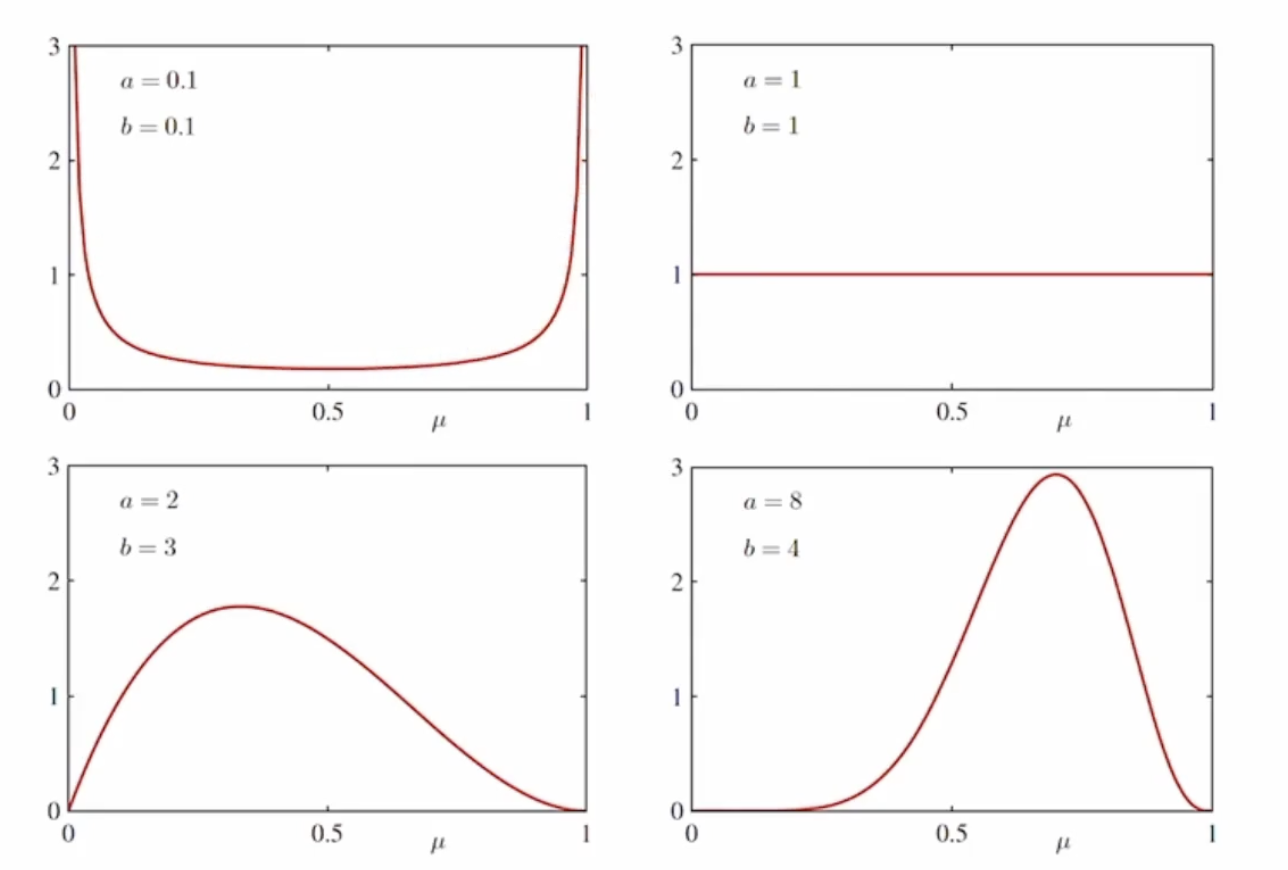
$ Beta( \mu | a, b ) = \frac{\Gamma(a+b) }{\Gamma(a) \Gamma(b)} \mu^{a-1}(1- \mu) ^{b-1} $
감마함수는 다음과 같이 정의 된다.
$ \Gamma = \int^{\infty}_0 u^{x-1}e^{-u} du $
감마 함수는 계승을 실수로 확장시킨다 . $ \Gamma (n) = (n -1 )! $
$ \Gamma(x) = (x-1) \Gamma(x-1) $ 임을 증명하기
Using intergration by parts $ \int ^{\infty} _{0} adb = ab|^{\infty}_{0} - \int^{\infty}_{0} bda $
$ a = \mu^{x-1} $ $ db = -e^{-u} du $
$ b = e ^{-u} $ $ da = (x - 1)u^{x-2} du $
$ \Gamma(x) = \mu^{x-1} ( -e ^{-u})|^{\infty}_{0} + \int^{\infty}_{0} (x-1) \mu ^{x-2} e^{-u} du $
$ = 0 + ( x - 1 ) \Gamma (x - 1 ) $
베타분포가 nrmailzed 일을 증명하기 $( \int ^{\mu | a, b) d \mu = 1 )$
$ \int^{1} _{0} \mu ^ {a-1}(1 - \mu)^{b-1} d \mu = \frac{\Gamma (a) \Gamma(b) } {\Gamma(a + b)}$임을 증명하면 된다.
$ \Gamma(a) \Gamma(b) = \int ^{\infty}_{0} x ^{a-1} e^{-x} dx \int ^{\infty}_{0} y^{b-1} e^{-y} dy $
$ = \int ^{\infty}_{0} \int ^{\infty}_{0} e^{-x-y}x^{a-1}y^{b-1}dydx $
$ = \int ^{\infty}_{0} \int ^{\infty}_{0} e^{-t} x^{a-1}(t-x)^{b-1} dtdx $ $ by t = y+x, dt = dy$
$ = \int ^{\infty}_{0} \int ^{\infty}_{0} e^{-t} x^{a-1}(t-x)^{b-1} dxdt $
$ = \int ^{\infty}_{0} d^{-t} \int ^{\infty}_{0} x^{a-1}(t-x)^{b-1} dxdt $
$ = \int ^{\infty}_{0} d^{-t} \int ^{\infty}_{0} (t \mu )^{a-1}(t-t \mu )^{b-1} td\mu dt $ $ by x = t\mu ,dx= td\mu $
$ = \int ^{\infty}_{0} e^{-t}t^{a-1}t^{b-1}t \left ( \int^1 _0 \mu^{a-1}(1- \mu)^{b-1} d \mu \right ) dt $
$ = \int ^{\infty}_{0} e^{-t}t^{a+b-1}dt \int^1 _0 \mu^{a-1}(1- \mu)^{b-1} d \mu $
$ = \Gamma (a+b) \int^{1}_{0} \mu^{a-1}(1 -\mu )^{b-1} d \mu $
따라서, $ \int^1_0 \mu^{a-1} (1-\mu)^{b-1} d\mu = \frac{\Gamma(a) \Gamma (b)}{\Gamma(a + b)} $ 이 성립한다.
이해하신분 뎃글좀
#(데이터를 m 이나 l 로 표현 )
$ \mu$ 에 사후확률
$ p( \mu | m , l , a, b ) = \frac{Bin(m| N, \mu )Beta(\mu |a,b)}{\int^1_0 Bin(m|N, \mu) Beta( \mu| a,b)d \mu } $
$ = \frac {\mu ^{m+a-1} (1- \mu ) ^{l +b -1 } }{\int^1_0 \mu ^{m+b -1}(1- \mu)^{l+b -1} d \mu }$
$ = \frac {\mu ^{m+a-1} (1 -\mu) ^{l +b -1 } }{\Gamma (m+a) \Gamma( l+b)/ \Gamma(m + a + l + b) } $
$ = \frac { \Gamma(m + a + l + b) }{\Gamma (m+a) \Gamma( l+b)}\mu ^{m+a-1} (1 -\mu) ^{l +b -1 }$
예측분포
$ p(x = 1 | \mathcal{D} ) \int^1_0 p (x = 1 | \mu )p(\mu | \mathcal{D})d\mu = \int ^1_0 = \mu p (\mu | \mathcal{D}) d\mu = \mathbb{E}[ \mu | \mathcal{D} ] $
$ p(x=1| \mathcal{D} = \frac{m +a }{ m+a+l+b} $
D가 떨어저나간다는데 그런게 컨디셔널 비펜스라고 한다고 한다 근데 왜그런지 이해를 못함
2. 다항변수(Multinomial Variables) : 빈도주의 방법
K개의 상태를 가질수 있는 확률변수를 K차원의 벡터 x (하나의 원소만 1이고 나머지는 0)로 나타낼 수 있다.
이런 x를 위해서 베르누이 분포를 다음과 같이 일반화 시킬 수 있다.
$ \prod ^{K} _{k=1} \mu ^{x_k} _{k} $
$ with \sum _{k} \mu_{k} = 1 $
x의 기댓값
$ \mathbb{E}[x| \mu ] = \sum _{x} p(x| \mu ) = ( \mu _1 , ... , \mu _M ) ^ T = \mu $
우도함수
x값을 N번 관찰한 결과 $ \mathcal{D} = \{ x_1, ... , x_N \} $ 가 주어쩟을 때, 우도함수는 다음과 같다.
$ p(\mathcal{D} | \mu ) = \prod ^N _{ n=1 } \prod ^K _{ k=1 } \mu ^{x_{nk}}_k = \prod ^K _{ k=1 } \mu ^{\sum _n x_{ nk} )}_k = \prod ^K _{ k=1 }\mu^{m_k} _k $
$ m_k = \sum _n x_{nk} $
$ \mu $ 최대우도 추정치(mixmum likelihood estimate)를 구하기 위해선 $ \mu_k $ 의 합이 1이 된다는 조건하에서 $ln p(\mathcal{D}| \mu ) $을 최대화 시키는 $ \mu _k $ 를 구해야 한다. 라그랑주 승수 $ \lambda $ 를 사용햐소 다음을 최대화 시키면 된다
$ \sum ^{K} _{k=1} m_k ln \mu _k + \lambda \left ( \sum ^ {K} _ {k=1} \mu_k -1 \right ) $
$ \mu ^{ML} _{k} = \frac{m_k}{N} $
다항분포
파라미터 $ \mu $ 와 전체 관찰개수 N 이 주어져씨을 때 $ m_1 , ..., m_k $의 분포를 다항분포 이라고 하고 다음과 같은 형태를 가진다.
$ Mult(m_1, ... , m_k | \mu , N ) = \binom{N}{m_1m_2...m_k} \prod ^{K} _{k=1} \mu^{m_k}_k $
$ \binom{N}{m_1m_2...m_k} = \frac{N!}{m_1!m_2! ... m_k! }$
$ \sum ^K_{k=1} m_k = N $
디리클레 분포 : 다항분포를 위한 켤레사전분포
$ Dir(\mu | \alpha ) = \frac{ \Gamma _{\alpha_0}}{\Gamma _{\alpha_1} ... \Gamma _{\alpha_K} } \prod ^{K}{ k=1 } \mu^{a_k -1 }_k $
$ \alpha_0 = \sum ^K _{k=1} \alpha _k $
디리클레 분포가 노멀라이즈 되는것을 증명
다음 결과를 사용한다
$ \int ^U_L (x-L)^{a-1}(U-x)^{b-1} dx = \int ^1 _0 (U -L ) ^{a-1} t ^{a-1} ( U - L ) ^{b-1} (1-t)^{b-1} (U-L)dt $ $by t = \frac{ x- L} {U -L}$
$ = (U-L) ^{a+b-1} \int ^1_0 t^{a-1}(1-t)^{b-1} dt $
$ = (U-L) ^{a+b-1} \frac{\Gamma (a) \Gamma (b) }{ \Gamma (a+b) } $
$ \int ^{1- \mu_1 } _0 \mu ^{\alpha_1 -1} _{1} u^{\alpha_2 -1}_{2} (1- \mu_1 - \mu_2)^{\alpha _3 -1} d \mu _2 = \mu ^{\alpha_1 -1} _{1} \int ^{1- \mu_1 } _0 u^{\alpha_2 -1}_{2} (1- \mu_1 - \mu_2)^{\alpha _3 -1} d \mu _2 $ $by L = 0 , U = 1 - \mu _1 $
$ = \mu ^{\alpha_1 -1 } _1 (1-\mu_1)^{\alpha_2 + \alpha_3 -1 }\frac{\Gamma(\alpha_2) \Gamma(\alpha_3)}{\Gamma(\alpha_2+\alpha_3)}$
$\int ^{1} _0 \int ^{1- \mu_1 } _0 \mu ^{\alpha_1 -1} _{1} u^{\alpha_2 -1}_{2} (1- \mu_1 - \mu_2)^{\alpha _3 -1} d \mu _2 d \mu _1 = \frac{\Gamma(\alpha_2) \Gamma(\alpha_3)} {\Gamma(\alpha_2+\alpha_3)} \int ^1_0 \mu ^{\alpha _1 - 1 }_1(1 - \mu_1)^{\alpha_2 +\alpha_3 -1}d\mu_1 $
$ = \frac{\Gamma(\alpha_2) \Gamma(\alpha_3)} {\Gamma(\alpha_2+\alpha_3)} \frac{\Gamma(\alpha_1) \Gamma(\alpha_2 + \alpha_3)} {\Gamma(\alpha_1+\alpha_2+\alpha_3)} $
$ \frac{\Gamma(\alpha_1) \Gamma(\alpha_2) \Gamma(\alpha_3) } {\Gamma(\alpha_1+\alpha_2+\alpha_3)} $
다항변수 베이지언 방법
일반적인 경우 (K= M ) : 귀납법 으로 증명
$ \mu $ 의 사후확률
$ p(\mu | \mathcal(D) ,\alpha ) = Dir(\mu | \alpha + m ) $
$ = \frac{ \Gamma (\alpha _0 + N }{ \Gamma (\alpha _1 + m_1 ) ... \Gamma (\alpha _K + m_K )} \prod ^{K} _ {k=1} \mu ^{\alpha_ k + m_ k - 1 } _k $
$ m = ( m_1, ... , m_k )^T $
$ \alpha _k $를 $ x_k = 1 $ 에[대한 사전관찰 개수라고 생각할 수 있다.
'Programmers > 데브코스 인공지능' 카테고리의 다른 글
| [프로그래머스 스쿨 AI] Weak 6 머신러닝 기초 수학 (0) | 2021.06.07 |
|---|---|
| [프로그래머스 스쿨 AI] Weak 6 E2E 실습 집값에 따른 분석 (0) | 2021.06.06 |
| [프로그래머스 스쿨 AI] Weak 6 선형회귀 실습 (0) | 2021.06.03 |
| [프로그래머스 스쿨 AI] Weak6 결정이론 (0) | 2021.06.01 |
| [프로그래머스 스쿨 AI] Weak 6 확률이론 (0) | 2021.05.28 |