1. 확률 변수( Random Variable)
대문자 X, Y : 확률 변수
소문자 x, y : 확룰 변수가 가질 수 있는 값
확률 P(확률)는 집합 S의 부분집합을 실수값에 대응시키는 함수
P[X =x] 확률변수 X가 x값을 가질 확률?
P[ X < x] 확률변수 X가 x보다 작을 확률?
X = x, X < x
2. 연속확률 변수
누적분포함수(cumulative distribution function, CDF): $ F(x) = P[X \in ( - \infty , x)] $
누적분포함수 F(x)를 가진 확률변수 X에 대해서 다음을 만족하는 함수 $ f(x) $ 가 존재한다면 X를 연속확률 변수라고 부르고 $ f(x) $ 를 X의 확률밀도함수라고 부른다
$ f(x) = \int ^x _\infty f(t)dt$
확률 변수를 명확히 하기 위해 $ F_X(x), fx(x) $로 쓰기도 한다
혼란이 없을경우 $ f_X(x) $ 대신 $p_X(x), p_x(x), p(x)를 사용하기도 한다.
$ p(x) \geq 0, \int ^\infty _{- \infty} p(x) =1 $
3. 확률변수의 성질
1.덧셈법칙
$p(X) = \sum _Y p(X, Y) $
2. 곱셈법칙
$ p(X, Y) = p(X|Y)p(Y) = p(Y|X)p(X)$
3.베이즈 확률 :
$ P(Y|X) = \frac{p(X|Y)p(Y)}{\sum_Y p(X|Y)p(Y)}$
$ posterior = \frac{likelihood \times prior}{normalization} $
posterior : 사후확률
likelihood : 가능도(우도)
prior : 사전확률
normaliztion : Y와 상관없는 상수. X의 경계확률(margina) p(X)
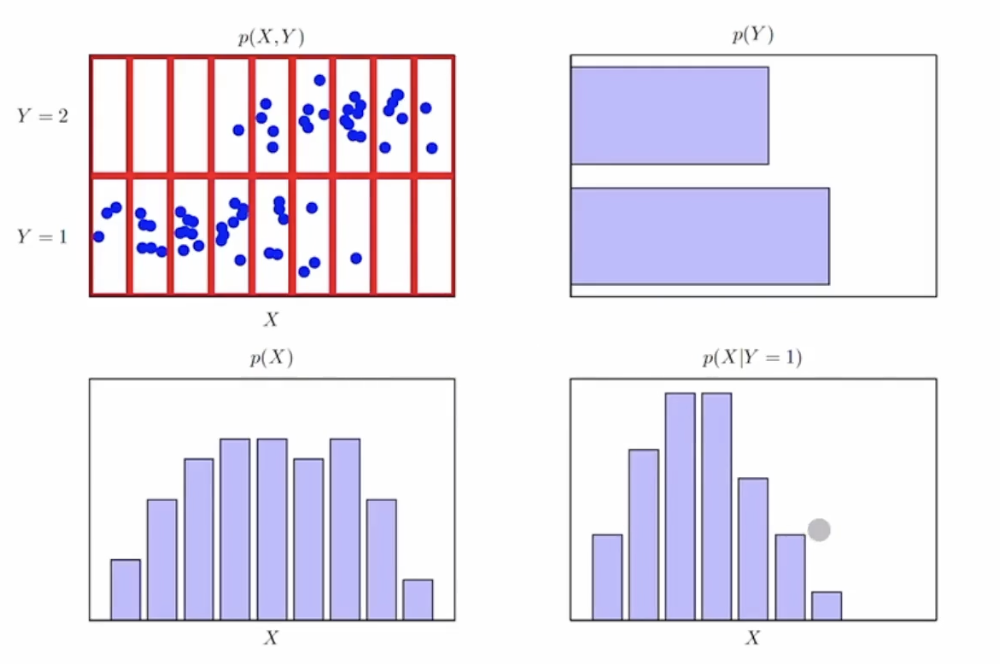
그림으로 보니깐 편하다
4. 확률변수의 함수
확률변수 $ X $ 의 함수 $ Y = g(X) $ 와 역함수 $w(Y) = X $가 주어졌을 때 다음이 성립한다.
$ p_y(y) = p_x(x)|\frac{dx}{dy}|$
k차원의 확률변수 벡터$ x = (x_1, ... , x_k) $ 가 주어졌을 때 , k개의 x에 관한 함수들 $ y_i = g_i(x) for i = 1, ... , k $ 는 새로운 확률변수벡터 $ y = (y_1 ,...,y_k) $를 정의 한다 간략하게$ y =g(x)$로 나타낼 수 있다.
만약 $ y= g(x) $ 가 일대일 변환인 경우 $ (x = w(y)로 유일한 해를 가질 때), y 의 결합확률밀도함수 는
$ p_y(y_1, ..., y_k) = p_x(x_1, ..., x_k)|J| $
야코비안 $J = \begin{bmatrix}
\frac{dx_1}{dy_1} & \frac{dx_1}{dy_2} & \cdots &\frac{dx_1}{dy_k} \\
\frac{dx_2}{dy_1} & \ddots & & \vdots \\
\vdots & & & \\
\frac{dx_k}{dy_1} & \cdots & & \frac{dx_k}{dy_k}
\end{bmatrix}$
예제
$P_{x_1,x_2}(x_1,x_2) = e^{-(x_1 +x_2)}, x_1 >0, x_2 >0 $ 라고 하자
$ y_1 = x_1, y_2 = x_1 + x_2 $ 에 의해서 정의되는 y의 pdf는?
$ x_1 = y_1 , x_2 = y_2 - y_1 $
J =
$ \begin{bmatrix}
1 & 0\\
-1 & 1
\end{bmatrix}$
간단히
서로 상관이 없으면 0
상관이 있으면 값 구하기
행렬곱을 구하면 대각선 끼리 곱하니깐
1이 된다
$ f_{y_1,y_2} (y_1,y_2) = f_{x_1,x_2}(x_1, x_2) |J| = f_{x_1,x_2}(y_1, y_2 -y_1 ) = e^-{y_1 +(y_2-y_1)} = e^{-y_2} $
그리고
$ y_1 = x_1 $ 인데 $ x_1 > 0 $ 이니깐 $ y_1 = ($어떤값$> 0)$
$ y_2 = x_1 + x_2 $ 인데 $ x_1 = y_1 , x_2 > 0 $ 이니깐 $ y_2 = y_1 + ($어떤값$ >0) $ y_2 > y_1 $
이렇게 된다
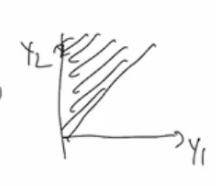
그러면
이러한 그림의 영역이되고
이것을 위에 지수로그에 넣으면
$ f_{y_1} (y_1) = \int ^\infty _ {y_1} e^{-y2}dy_2 = e^{- \infty} - (e^{-y_1}) = -e^{-y_1} $
CDF Technique
확률변수 X가 CDF F_X(x)를 가진다고 하자. 연속확률분포함수 U ~ UNIF(0,1) 의 함수 정의되는 다음확률변수 Y를 생각해보자.
$ Y = F^{-1} _X (U) $
확률변수 Y는 확률변수 X와 동일한 분포를 따르게 된다.
$ F_Y(y) = P[Y \leq y] $
$= P[F_X ^{-1} (U) \leq y] $
$= P[U \leq F_X(y)] $
$= F_X(y) $
# smapling random points within a circle with radius r
# inverse transform sampling
# cdf: F(d) = d**2 /. r**2
# inverse cdf : r * (u**0.5)
import turtle
import math
import random
wn = turtle.Screen()
alex = turtle.Turtle()
alex.hideturtle()
r = 200
for i in range(5000):
u = random.random()
d = r * (u**0.5)
theta = random.random()*360
x = d * math.cos(math.radians(theta))
y = d * math.sin(math.radians(theta))
alex.penup()
alex.setposition(x, y)
alex.dot()
turtle.update()
wn.mainloop()여기서 u를 루트를 씨운이유는 1보다 작을때는 루트를 하면 자연수에서 제곱한것과 같게되기때문이다
5. 기댓값 (Exoectations)
기대값 : 확률분포 p(x)하에서 $ f(x) $ 의 평균값
이산확률분포 : $ \mathbb{E} [f] \approx \frac{1}{N} \sum^N_{n=1}f(x_n) $
연속확률분포 : $ \mathbb{E} [f] = \int p(x)f(x)dx $
여러개 변수들의 함수
$ \mathbb{E}_x [f(x,y)] = \sum_{x}f(x,y)p(x) $
y 에 대한 함수임을 상기할것
$ \mathbb{E}_{x,y} [f(x,y)] = \sum_{y}\sum_{x}f(x,y)p(x,y) $
조건부 기댓값
$ \mathbb{E}_{x} [f|y] = \sum_{x}f(x)p(x|y) $
이것에 대하여는
6. 분산(variance), 공분산(covariance)
$ f(x) $. 의 분산(variance): $ f(x) $ 의 값들이 기댓값 $ \mathbb{E} [f] $ 으로부터 흩어져 있는 정도
$ var[f] = \mathbb{E}[(f(x) - \mathbb{E}[f(x)])^2] = \mathbb{E}[f(x)^2] - \mathbb{E}[f(x)]^2 $
$ var[x] = \mathbb{E}[x^2] - \mathbb{E}[x]^2 $
두 개의 확률변수 x,y에 대한 공분산(covariance)
$ cov[x,y] = \mathbb{E}_{x,y}[\{x-E[x]\}\{y - \mathbb{E}[y]\}] $
$ = \mathbb{E}_{x,y}[xy] - \mathbb{E}[x]\mathbb{E}[y]$
$ X,Y $ 가 각각 확률변수의 벡터라고 할 때
$ cov[X,Y] = \mathbb{E}_{X,Y}[\{X-E[X]\}\{Y^T - \mathbb{E}[Y^T]\}] $
$ = \mathbb{E}_{X,Y}[XY^T] - \mathbb{E}[X]\mathbb{E}[Y^T] $
cov[X] =cox[X,X]
7.빈도주의 대 베이지안
확률을 해석하는 두가지 다른 관점 : 빈도주의 (frequentist), 베이지안(Bayesian)
빈도주의 : 반복가능한 사건들의 빈도수에 기반
베이지안: 불확실성을 정량적으로 표현
모델의 파라미터 w(예를 들어 다항식 곡선 근사문제에서의 계수 w)에 대한 우리의 지식을 확률적으로 나타내고 싶다면?
w에 대한 사전지식 $p(2) \Rightarrow $ 사전확률(prior)
새로운 데이터 $D = {t_1 ,... , t_N } $ 를 관찰하고 난뒤의 조선부확률 $ p(D|w) \Rightarrow $ 우도함수(likelihood funtion).특정 w 값에 대해 $D$ 의 관찰값이 얼마나 가능성이 있는지를 나타냄. W에관한함수임을 기억할것
$ p(w|D) = \frac{p(D|w)p(w)}{p(D)} $
p(w|D) 는 D 관찰하고 난 뒤의 w에 대한 불확실성을 표현
사후확룰(posterior) $ \propto $ 우도 (likelihood) $ \times $ 사전확률(prior)
반면, 빈도주의는 w가 고정된파라미터이고 최대우도와 같은 '추정자'를 사용해서 그 값을 구한다. 구해진. 파라미터의 불확실성 부트스트랩 방법을 써서 구할수 있다
베이지안 관정의 장점
사전확률을 모델에 포함시킬 수 있다.
동전을 던져서 세번마다 앞면이 나왔을때
최대우도 : 앞면이 나올확률은 1이됨
베이지안: 극단적인 확률을 피할 수 있음
8. 정규분포 (Gaussian Distribution)
단일변수 x를 위한 가우시안 분포
$ \mathcal{N}(x| \mu , \sigma ^2) = \frac{1}{2\pi \sigma ^{1/2}} exp\{-\frac{1}{2\sigma^2}(x -\mu)^2\} $
가우시안 분포가 정규화됨 (normaliazed)를 보일 것임. 즉,
$ \int ^ {\infty } _{-\infty } \mathcal{N} (x | \mu,\sigma^2)dx =1 $
정규분포 : 정규화(Normaliztion)
$ I = \int ^ {\infty } _{-\infty } exp(-\frac{1}{2 \sigma ^2}x^2) dx $
$ I^2 = \int ^ {\infty } _{-\infty } \int ^ {\infty } _{-\infty } exp(-\frac{1}{2 \sigma ^2}(x^2+ y^2)) dxdy $
$ = \int ^ {2\pi } _{0 } \int ^ {\infty } _{0} exp(-\frac{1}{2 \sigma ^2}(r^2)) rdrd\theta $
$ = \int ^ {2\pi } _{0 } \{-\sigma ^2 exp(-\frac{1}{2 \sigma ^2}r^2) |^{\infty}_{0} \}d\theta $
$ = \int ^{2\pi}_{0} \sigma^2 d\theta $
$ = 2 \pi \sigma^2 $
$ I = \sqrt{2 \pi \sigma^2} $
정규분포 기댓값
$ \mathbb{E} = \int ^ {\infty } _{-\infty } \mathcal{N} (x | \mu,\sigma^2)xdx $
$ \mathbb{E} = \int ^ {\infty } _{-\infty } \frac{1}{\sqrt {2 \pi \sigma^2 }} exp\{ -2 \frac{1}{2\sigma^2} (x- \mu )^2 \} xdx $
$ \mathbb{E} = \int ^ {\infty } _{-\infty } \frac{1}{\sqrt {2 \pi \sigma^2 }} exp\{ -2 \frac{1}{2\sigma^2} y^2\}(y+\mu) dy $
$ \mathbb{E} = \int ^ {\infty } _{-\infty } \frac{1}{\sqrt {2 \pi \sigma^2 }} exp\{ -2 \frac{1}{2\sigma^2} y^2\}ydy + \mu \int ^ {\infty } _{-\infty } \frac{1}{\sqrt {2 \pi \sigma^2 }} exp\{ -2 \frac{1}{2\sigma^2} y^2\}dy$
$ 0 + \mu \cdot 1 $
= $ \mu $
정규분포 분산
$ \frac{d}{dy} \int ^{\infty}_{-\infty} \mathcal{N}(x|\mu, y)dx = 0 $
$ \frac{d}{dy} \int ^{\infty}_{-\infty} \{\frac{1}{\sqrt{2\pi y}} exp\{-\frac{1}{2y}(x - \mu )^2\}dx $
$ = \int ^{\infty}_{-\infty} \{( \frac{d}{dy} \frac{1}{\sqrt{2\pi y}}) exp\{-\frac{1}{2y}(x - \mu )^2\} + \frac{1}{\sqrt{2\pi y}}( \frac{d}{dy}exp\{-\frac{1}{2y}(x-\mu)^2\})\}dx $
$ = -\frac{1}{2}\frac{1}{\sqrt{2\pi}}y^{-3/2} \int ^{\infty}_{-\infty} exp\{-\frac{1}{2y}(x - \mu )^2\}dx + \frac{1}{2y^2}exp\{-\frac{1}{2y}(x - \mu )^2\}dx $
$ = -\frac{1}{2}\frac{1}{\sqrt{2\pi}}y^{-3/2}\sqrt{2 \pi y} + \frac{1}{2y^2}var[x]\ $
$ =-\frac{1}{2y} + \frac{1}{2y^2}var[x] $
$ var[x] = y = \sigma^2 $
위는 공부더해야함 모르겟음
정규분포 최대우도해
$ X = (X_1 ,..., x_N)^T $ 가 도립적으로 같은 가우시안분포로부터 추출된 N개의 샘플들이 라고 할 때,
$ p(X| \mu, \sigma^2 ) = p(x_1, ... , x_N| \mu, \sigma ^2) = \prod^{N} _{n=1} \mathcal{N} (x_n|\mu ,\sigma ^2) $
$ ln p(X|\mu,\sigma ^2) = -\frac{1}{2\sigma^2} \sum^{N}_{n=1} (x_n - \mu)^2 - \frac{N}{2}ln\sigma^2 - \frac{N}{2}ln(2\pi) $
$ \frac {\partial}{\partial\mu}ln p(X|\mu, \sigma^2) $
$ = \frac {\partial}{\partial\mu} \{-\frac{1}{2\sigma^2} \sum ^N _{n=1} (x_n - \mu)^2 - \frac{N}{2}ln \sigma^2 - \frac{N}{2}ln(2\pi) \} $
$ = \frac {\partial}{\partial\mu} \{-\frac{1}{2\sigma^2} \sum ^N _{n=1} (x_n - \mu)^2 - \frac{N}{2}ln \sigma^2 - \frac{N}{2}ln(2\pi) \} $
$ = \frac{1}{\sigma^2}\{(\sum^{N}_{n=1} x_n)-N_{\mu} \} $
$ \mu_{ML} = \frac{1}{N}\sum^{N}_{n=1} x_n $
분산값:??
$ y= \sigma^2 $
$ \frac {\partial}{\partial\mu}ln p(X|\mu, y) $
$ = \frac {\partial}{\partial y} \{-\frac{1}{2}y^{-1} \sum ^N _{n=1} (x_n - \mu_{ML})^2 - \frac{N}{2}ln y - \frac{N}{2}ln(2\pi) \} $
$ = \frac{1}{2}y^{-2} \sum ^{N}_{n=1} (x_n - \mu _{ML})^2 - \frac{N}{2}y^{-1} $
$ y_{ML} = \sigma^2_{ML} = \frac{1}{N} \sum^{N}_{n=1}(x_n - \mu_{ML})^2 $
곡선 근사 (Curve Fitting) : 확률적 관점
학습데이터 : $ X = (x_1, ... , x_N)^T , t = (t_1, ... , t_N)^T $
목표값 t 의 불확실성을 다음과 같이 확률 분포로 나타낸다.
$ p(t|x,w,\beta ) = \mathcal{N} (t|y(x,w),\beta^{-1} $
파라미터 : w, \beta
파라미터들의 최대우도해를 구해보자.
우도함수
$ p(t|X, w,\beta) = \prod ^N _{n=1} \{y(x_n,w) -t_n \} \beta ^{-1} $
로그우도함수
$ln p (t|X,w,\beta ) = - \frac{\beta}{2} \sum ^N _ {n=1} \{ y(x_n,w) -t_m\}^2 - \frac{N}{2}ln\beta - \frac{N}{2} ln(2\pi) $
w에 관해서 우도함수를 최대화 시키는 것은 제곱합 오차함수 를 최소화 시키는 것과 동일
$ \beta $의 최대우도해
$ \frac{1}{\beta_{ML}} = \frac{1}{N} \sum ^{N}_{n=1}\{y(x_n,w_{ML})-t_n\}^2 $
예측분포
$ p (t|x, w_{ML}, \beta_{ML} )= \mathcal(t|y(x,w_{ML}),\beta^{-1}_{ML} $
사전확룰 포함
파라미터 w 의 사전확률을 다음과 같이 가정하자
$ p(w|\alpha ) = \mathcal{N} (w|0, \alpha^{-1}I) = (\frac{\alpha}{2\pi})^{(M+1)/2}exp\{-\frac{\alpha}{2}w^Tw\} $
w의 사후확률은 우도함수와 사전확률의 곱에 비례한다.
$ p(w|X, t, \alpha, \beta ) \propto p(t|X, W,\beta )p(w|\alpha) $
이 사후확률을 최대화시키는 것은 아래 함수를 최소화 시키는 것과 동일하다.
$ \frac{\beta}{2}\sum^N_{n=1} \{ y(x_n,w) - t_n\} ^2 + \frac{\alpha}{2}w^TW $
이것은 규제화된 제곱합 오차 함수를 최소화 시키는 것과 동일하다 ($ \lambda = \alpha | \beta $).
최종단계 : 완전한 베이지안 곡선 근사
이제까지 t의 예측분포를 구하기 위해 여전히 w의 점추정에 의존해왔다, 완전한 베이지안 방법은 w의 분포로 부터 확률의 기본법칙만을 사용해서 t 의 예측분포를 유도한다.
$ p(t|x,X,t) = \int p(t|x,w)p(w|X,t)dw $
이 예측분포도 가우시안 분포라는 사실과 그분포의 평균벡터와 공분산 행렬을 구하는 방법을 다음에 알아볼 것이다.
'Programmers > 데브코스 인공지능' 카테고리의 다른 글
| [프로그래머스 스쿨 AI] Weak 6 선형회귀 실습 (0) | 2021.06.03 |
|---|---|
| [프로그래머스 스쿨 AI] Weak6 결정이론 (0) | 2021.06.01 |
| [프로그래머스 스쿨 AI] Weak 6 머신러닝이란 1 (0) | 2021.05.28 |
| [프로그래머스 스쿨 AI] Weak 5 Django + uwsgi+ nginx + aws 완전 삭제후 따라해보기 드뎌! 배포 됫다 (0) | 2021.05.21 |
| [프로그래머스 스쿨 AI] Weak 5 Django DB, forms (0) | 2021.05.19 |
