1. 결정이론이란?
새로운 값 x가 주어졌을때 확률모델 p(x,t) 에 기반해 최적의 결정(예를 들어 분류)을 내리는 것
추론 단계 : 결합확률분포 $ p(x, C_k)$ 를 구하는 것 $ (p(C_k|x)$ 를 집적 구하는 경우도 있음). 이것만 있으면 모든 것을 할 수 있음.
결정단계 : 상황에 대한 확률이 주어졌을 때 어떻게 최적의 결정을 내릴 것인지? 추론단계를 거쳤다면 결정단계는 매우 쉬움.
예제: X-Ray의 이미지로 암판별
x:X-Ray 이미지
$C_1 $ : 암인 경우
$C_2 $ : 암이 아닌 경우
$p(C_k|x) $의 값을 알기 원함
$ p(C_k|x)= \frac{p(x,C_k)}{p(x)} $
$ =\frac{p(x,C_k)}{\sum^2_{k=1}p(x,C_k)}$
$ =\frac{p(x|C_k)p(C_k}{p(x)} $
$\propto$우도(likelihood) $\times$ 사전확률(prior)
직관적으로 볼때 p(C_k|x)를 최대화 시키는 k를 구하는 것이 좋은 결정
2. 결정이론 이진 분류
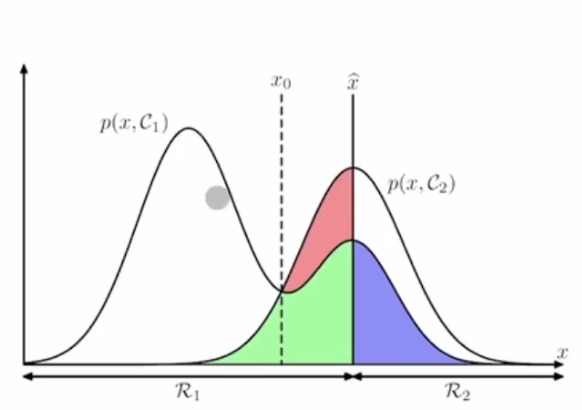
결정영역
$ \mathcal{R}_i \{x : pred(x) = C_i\} $
분류오류 확률 (probability of misclassification)
$ p(mis) = p(x \in \mathcal{R}_1, C_2) + p(x \in \mathcal{R}_2,C_1) $
$ = \int _{\mathcal{R}_1} p(x,C_2)dx + \int _{\mathcal{R}_2}p(x,C_1)dx $
오류를 최소화 하려면 다음조건을 만족하면 x를 $\mathcal{R}_1$d에 할당해야한다.
$p(x,C_1) > p(x,C_2)$
$ \Leftrightarrow p(C_1|x)p(x) > p(C_2|x)p(x) $
$\Leftrightarrow p(C_1|x) > p(C_2|x) $
다중분류
$ p(correct) = \sum^K_{k=1}p(x \in \mathcal{R}_k,\mathcal{C}_k) $
$ = \sum^K_{k=1} \int _{\mathcal{R}_k} p(x , \mathcal{C}_k)dx $
$ pred(x) = argmax_kp(C_k|x) $
밑에 유튜버의 이진 다중 분류에 대한 설명을 들으면 이해가 편하다
결정이론의 목표 (분류의 경우)
결합확률분포 $p(x, C_k) $ 가 주어졌을때 최적의 결정영역들 R_1, ... , R_k 를 찾는 것
$ \hat{C}(x) $를 x 가 주어졌을때 예측값(1,...,K중의 값) 을 돌려주는 함수라고 하자
$ x\in \mathcal{R}_j \Leftrightarrow \hat{C}(x) = j $
결합확률 분포 p(x, C_k) 가 주어졌을 때 최적의 함수 $\hat{C}(x)$ 를 찾는 것
"최적의 함수" 는 어떤 기준으로?
2. 기대 손실 최소화
모든 결정이 동일한 리스크를 갖는 것은 아님.
암이 아닌데 암인 것으로 진단
암이 맞는데 암이 아닌 것으로 진단
손실 행렬 (loss matrix)
$ L_{kj}:C_k $ 에 속하는 x 를 $ C_j $ 로 분류할 때 발생하는 손실 (또는 비용)
데이터에 대한 모든 지식이 확률 분포로 표현되고 있는 것을 기억할 것. 한 데이터 샘플 x의 실제 클래스를 결정론적으로 알고 있는 것이 아니라 그것의 확률만을 알 수 있다고 가정한다. 즉, 우리가 관찰할 수 있는 샘플(예를 들어, 암을 가진 환자의 X-Ray 이미지)은 확률분포 p(x, C_k) 를 통해서 생성된 것이라고 간주한다.
따라서 손실행렬 L이 주어졌을때 다음과 같은 기대손실을 최소화하는 것을 목표로 할 수 있다.
$ \mathbb{E} [L] - \sum _k \sum _j \int _{\mathcal{R}_j} L_{kj} p(x, C_k)dx $
$\hat{C}(x) $ 를 x가 주어졌을 때 예측값(1, ... , K 중의 값)을 돌려주는 함수 라고 하고
$x \in \mathcal{R}_j \Leftrightarrow \hat{C}(x) = j $
따라서 위의 $ \mathbb{E} [L]$ 식을 아래와 같이 표현할 수 있다
$ \int _{\mathcal{X}} \sum^K _{k=1}L_{k\hat{C}(x)}p(x,C_k)dx $
$ \int _{\mathcal{X}}( \sum^K _{k=1}L_{k\hat{C}(x)}p(C_k|x))p(x)dx $
이렇게 표현된 $mathbb{E}[L] $는$\hat{C}(x)$의 범함수 이고 이 범함수를 최소화 시키는 함수 $\hat{C}(x)를 찾으면 된다.
$ \hat{C}(x) = argmin_j \sum^K_{k=1} L_{kj}p(C_k|x) $
만약에 손실행렬이 0-1 loss인 경우 (주대각선 원소들은 0 나머지는 1)
$ \hat{C}(x) = argmin_j 1- p(C_k|x) $
$ =argmax_j p(C_j|x) $
예제 : 의료진단
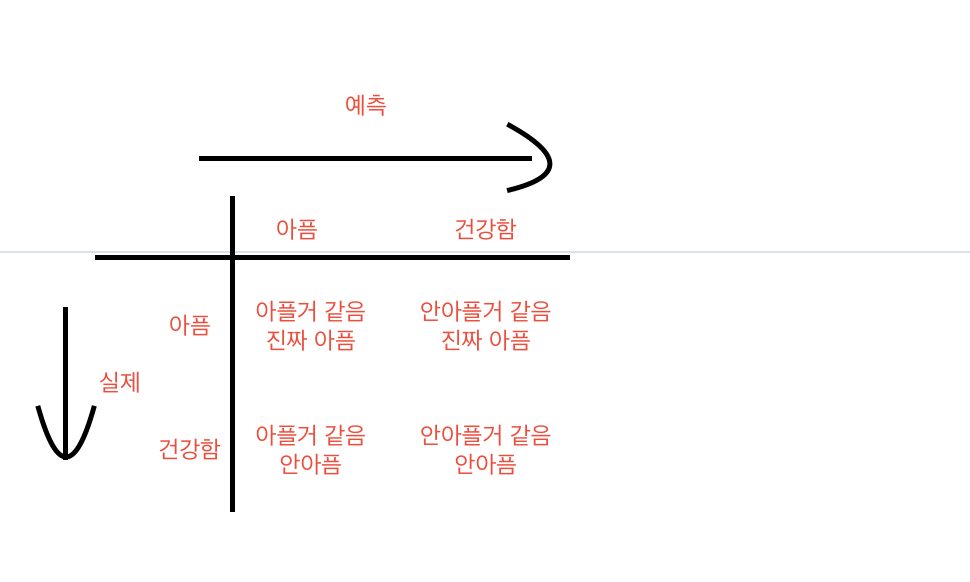
$C_k \in \{1,2\} \Leftrightarrow \{sick, healthy\}$
$L = \begin{bmatrix} 0 & 100 \\ 1 & 0 \end{bmatrix} $
이경우 기대 손실은
$ \mathbb{E} [L] = \sum_k \sum_j \int _{\mathcal{R}_j}L_{kj} p(x, C_k)dx $
$ = \int _{R_2} 100 \times p(x,C_1)dx + \int_{R_1} p(x,C_2)dx $
즉 저기 표에 얼마나 위험도를 넣을 거냐 이다 높을수록 안좋게 반영하는 것이다
결정이론 - 회귀문제의 경우
목표값 $ t \in \mathcal{R} $
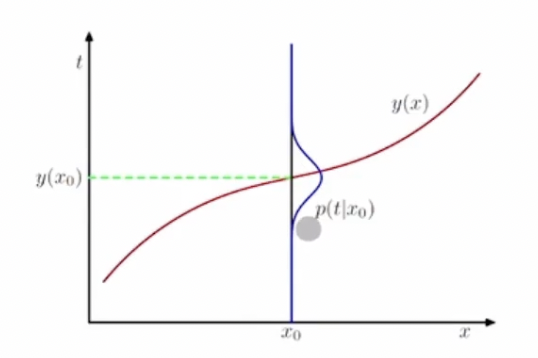
손실함수 :$ L(t,y(x)) = \{y(x)-t\}^2$
$F[y] = E[L] = \int_{\mathcal{R}} \int_{\mathcal{X}}\{y(x)-t \}^2 p(x,t)dxdt$
$= \int_{\mathcal{X}} ( \int_{\mathcal{R}}\{y(x)-t \}^2 p(x,t)dt)dx$
$= \int_{\mathcal{X}} ( \int_{\mathcal{R}}\{y(x)-t \}^2 p(t|x)dt)p(x)dx$
x를 위한 최적의 예측값은 $y(x) =\mathbb{E}_t[t|x] $임을 보일 것이다.
Euler-Lagrange Equation
$F[y] = \int^b_a G(x,y(x),y'(x))dx%
$ \frac{\partial F}{\partial y(x)} = \frac{\partial G}{\partial y} -\frac{d}{dx} \frac{\partial G}{\partial y'} $
For regression,
$ F[y] = E[L] = \int \int \{y(x) -t\}^2 p(x,t)dxdt $
$ = \int ( \int \{y(x) -t\}^2 p(x,t)dt)dx $
범함수 최소값을 구하는 문제
Euler-Lagrange 방정식에서의 G는
$ G = ( \int_{\mathcal{R}}\{y(x) -t\}^2 p(t|x)dt)p(x) $
$ \frac{\partial G}{\partial y} = p(x)\frac{\partial}{\partial y}( \int_{\mathcal{R}}\{y(x) -t\}^2 p(t|x)dt) $
$ \frac{\partial G}{\partial y} = 0 \Rightarrow \frac{\partial}{\partial y}( \int_{\mathcal{R}}\{y(x) -t\}^2 p(t|x)dt) = 0 $
$ \frac{\partial}{\partial y}( \int_{\mathcal{R}}\{y(x) -t\}^2 p(t|x)dt) = \frac{\partial}{\partial y}(y(x)^2 \int_{R}P(t|x)dt+2y(x) \int_{R} tp(t|x)dt + \int_R t^2p(t|x)dt) $
$ = \frac{\partial}{\partial y}(y(x)^2 + 2y(x) \mathbb{E}_t[t|x] + \int_R t^2p(t|x)dt) $
= 2y(x) - 2\mathbb{E}_t[t|x]
따라서 x 를 위한 최적의 예측값은
$y(x) = E_t[t|x]$
손실함수의 분해
$ (y(x) - t)^2 = \{ y(x) - \mathbb{E}[t|x] + \mathbb{E}[t|x]-t \}^2 $
$ \{ y(x) - \mathbb{E}[t|x] \}^2 +2\{y(x) - \mathbb{E}[t|x]\} \{ \mathbb{E}[t|x]-t \}+ \{ \mathbb{E}[t|x]-t \}^2 $
교차항(cross-tem)은 아래와 같이 사라진다.
$ 2 \int \int \{ y(x) - \mathbb{E}[t|x] \}\{\mathbb{E}[t|x] -t \}p(x,t)dxdt $
$= 2 \int \int \{ y(x) - \mathbb{E}[t|x] \}\{\mathbb{E}[t|x] -t \}p(t|x)p(x)dxdt $
$ 2 \int \{ y(x) - \mathbb{E}[t|x] \} p(x) ( \int \{ \mathbb{E}[t|x] - t \} p(t|x)dt)dx $
$ 2 \int \{ y(x) - \mathbb{E}[t|x] \} p(x) (\mathbb{E}[t|x] \int p(t|x)dt - \int tp(t|x)dt)dx $
$ 2 \int \{ y(x) - \mathbb{E}[t|x] \} p(x) (\mathbb{E}[t|x] - \mathbb{E}[t|x] )dx $
=0
따라서,
$ \mathbb{E}[L] = \int \{ y(x) - \mathbb{E}[t|x]\}^2 p(x)dx + \int var[t|x]p(x)dx $
함수 y(x) 는 첫번째 항에만 나타나며 그 값이 $ \mathbb{E}[t|x] $ 와 동일할 때 기대손실이 최소화 된을 알 수 있다.
두번째 항은 t의 분산(x에 대해 평균화된)이며 한수 y(x) 와 상관없다. 따라서 이 값은 더이상 줄일 수 없는 기대 손실의 최소값이다
3. 결정문제를 위한 몇가지 방법들
분류문제의 경우
확률모델에 의존하는 경우
생성모델 : 먼저 각클래스 $ C_k $ 에 대해 분포 $ p(x|C_k) $와 가전확률 $ p(C_k) $ 와 사전확률 $ p(C_k)$ 를 사용해서 사후확률 $ p(C_k|x) $ 를 구한다.
$p(C_k|x) = \frac{p(x|C_k)p(C_k)}{p(x)}$
p(X)는 다음과 같이 구할 수 있다.
$ p(x) = \sum_k p(x|C_k)p(C_k) $
사후확률이 주어졌기 때문에 분류를 위한 결정은 쉽게 이루어질 수 있다. 결합분포에서 데이터를 샘플링해서 "생성" 할 수 있으므로 이런 방식을 생성모델이라고 부른다.
식별모델 : 모든 분포를 다계산하지 않고 오직 사후확률 p(C_k|x)를 구한다. 위와 동일하게 결정이론을 적용할 수 있다.
판별함수에 의존하는 경우
판별함수 (discriminant function): 입력 x을 클래스로 할당하는 판별함수(discriminat function)를 찾는다. 확률값은 계산하지 않는다.
회기문제의 경우
결합분포 p(x,t) 를 구하는 추론 문제를 먼저 푼다음 조건부확률분포 p(t|x)를 구한다. 그리고 주변화를 통해 $ \mathbb{E}_t[t|x]$를 구한다
조건부확률분포 p(t|x)를 구하는 추론문제를 푼 다음 주변화를 통해 $ \mathbb{E}_t[t|x]$를 구한다.
y(x)를 직접적으로 구한다.
'Programmers > 데브코스 인공지능' 카테고리의 다른 글
| [프로그래머스 스쿨 AI] Weak 6 E2E 실습 집값에 따른 분석 (0) | 2021.06.06 |
|---|---|
| [프로그래머스 스쿨 AI] Weak 6 선형회귀 실습 (0) | 2021.06.03 |
| [프로그래머스 스쿨 AI] Weak 6 확률이론 (0) | 2021.05.28 |
| [프로그래머스 스쿨 AI] Weak 6 머신러닝이란 1 (0) | 2021.05.28 |
| [프로그래머스 스쿨 AI] Weak 5 Django + uwsgi+ nginx + aws 완전 삭제후 따라해보기 드뎌! 배포 됫다 (0) | 2021.05.21 |
