1. 벡터의 표현
좌표계 없이 표현

V : 화살표로 표현
V의 크기 : 길이
V의 방향 : 방향
$u \cdot v = \left \| u \right \||\left \| V \right \| cos \theta$
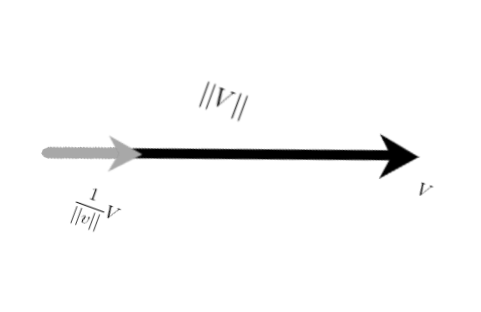
좌표계를 도입하여 표현
방향 : 길이는 1일때 그것이 방향이 된다 (백터($x^2,y^2$)들의 합 = 전체길이)
$u \cdot v = u_1v_1 + u_2v_2 + \cdots + u_1v_1 $
공식은
벡터의 크기와 방향 복습 (개념 이해하기) | 벡터 | Khan Academy
벡터의 크기와 방향에 대해 배운 지식을 이용하여 문제를 풀어 봅시다.
ko.khanacademy.org
좌표 벡터에 대한 사이트이다
직교할 경우
$u \cdot v = 0 \Leftrightarrow u\perp v$
2. 투영

두 벡터 u, a가 있을 때, 벡터 u를 위에 투영한 벡터를 $proj_au$라 하고 다음과 같이 구한다.
$proj_au = \left ( \frac{u\cdot a}{\left \| a \right \|} \right ) \left ( \frac{1}{\left \| a \right \|}a \right ) = \left ( \frac{u\cdot a}{\left \| a \right \|^2} \right ) a$
(용어:$proj_au$ = a를 x축으로 만든것이라고부른다
||v|| = $\sqrt{v_0^2+v_1^2+v_2^2 + \cdots +v_n^2}$)
이걸 참고하면 좀더 편하게 이해가 된다
3. 직교행열
1. 직교 행렬( orthogonal matrix)
$\begin{bmatrix}1 & 4\\ -2 & 2\end{bmatrix}
\begin{bmatrix}2 & 2 & -4\\ 2 & 1 & 7\\ 6 & -1 & -1\end{bmatrix}$
2. 정규 직교해렬( orhonormal matrix)
$\begin{bmatrix}
\frac{1}{\sqrt{5}} & \frac{2}{\sqrt{5}}\\
-\frac{2}{\sqrt{5}} & \frac{1}{\sqrt{5}}
\end{bmatrix}
\begin{bmatrix}
\frac{1}{\sqrt{11}} & \frac{2}{\sqrt{5}} & -\frac{4}{\sqrt{66}}\\
\frac{1}{\sqrt{11}} & \frac{1}{\sqrt{6}} & \frac{7}{\sqrt{66}}\\
\frac{3}{\sqrt{11}} & -\frac{1}{\sqrt{5}} & -\frac{1}{\sqrt{66}}
\end{bmatrix}$
계산 한걸 확인해보자
$x_i = \frac{b \cdot a_i}{\left \| a_i \right \|^2}$
일떄
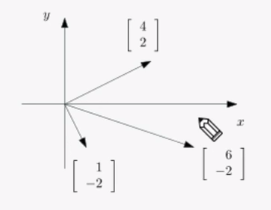
$\begin{bmatrix}1 & 4\\ -2 & 2 \end{bmatrix}\begin{bmatrix}x_1\\ x_2 \end{bmatrix}=\begin{bmatrix}6\\ -2\end{bmatrix} $
를 대입해보면
$
\begin{bmatrix}1 \\ -2 \end{bmatrix} x_1 + \begin{bmatrix} 4 \\
2 \end{bmatrix} x_2 = \begin{bmatrix}6\\ -2\end{bmatrix}
$
$\frac{\begin{bmatrix}6 \\-2 \end{bmatrix} \cdot \begin{bmatrix}1\\ -2\end{bmatrix}}{1^2 +(-2)^2}
= \frac{6\times 1+(-2)\times (-2)}{5}
\\x_1 = \frac{10}{5} $
$\frac{\begin{bmatrix}6 \\-2 \end{bmatrix} \cdot \begin{bmatrix}4\\ 2\end{bmatrix}}{4^2 +(2)^2}
= \frac{6\times 4+(-2)\times (2)}{20}
\\x_2 = \frac{20}{20}$
역행열을 구하지 않고 바로 계산이 가능하다
'Programmers > 데브코스 인공지능' 카테고리의 다른 글
| [프로그래머스 스쿨 AI] Weak 2 벡터공간과 최소제곱법 (이해아직안됨 준비중 ) (0) | 2021.04.28 |
|---|---|
| [프로그래머스 스쿨 AI] Weak 2 SVD,PCA (0) | 2021.04.28 |
| [프로그래머스 스쿨 AI] Weak 2 좌표계 (아직입니다) (0) | 2021.04.27 |
| [프로그래머스 스쿨 AI] Weak 2 행렬연산과 선형조합 (0) | 2021.04.26 |
| [프로그래머스 스쿨 AI] Weak 2 LU 분해 (0) | 2021.04.26 |
